Mat 301 Quiz 2 Differential Calculus

Welcome to my Mat 301 Calculus I site!

Quiz 2

Sample Questions

 

Question 1


f(x) = \arctan(3x - 3) + x + 1

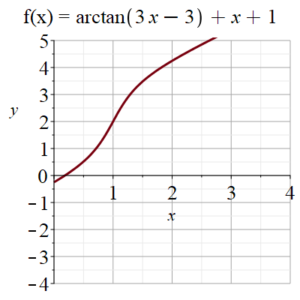
The graph of f is shown above. Find the equation of the tangent line to f at at   x = 1. Then, to get credit for Question 1,  find the y intercept of that tangent line to the nearest thousandth (3 decimal places).

Put the y coordinate of the y intercept on the line below.

Recall, the y intercept of the tangent line is where
the tangent line crosses the y axis.

Answer to Question 1:   the  y intercept of that tangent line  = \underline{\ \hspace{.75in}} .

Videos (3 parts) on how to solve Question 1.

Part 1.  Starting the problem and finding  f'(x) .

 

Part 2.  Evaluating f'(x_0) and finding the tangent line equation, and finally finding the y intercept (which is the answer to Question 1).

 

Part 3. Extra material. Finding the x intercept of that tangent line and graphing the tangent line.

 

Answer to Question 1:   the  y intercept of that tangent line  = \underline{\ \ -2.000 \ } .

Note. Here is a graph of that tangent line:

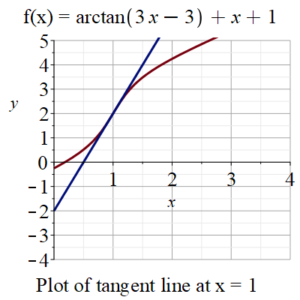
The following Maple commands will solve Question 1 and create the graph shown above.  You can copy and paste the following commands into Maple.

restart;
with(plots):
f := x -> arctan(3*x - 3) + x + 1;
"Find tangent line equation at";
x0 := 1;
xStart := 0:
xFinish := 4:
yStart := -4:
yEnd := 5:
TangentLine := (f, x0, x) -> D(f)(x0)*(x - x0) + f(x0):
"tangent line equation y  = mx +b";
evalf(TangentLine(f, x0, x));
"x intercept";
solve(evalf(TangentLine(f, x0, x)), x);
plot([f(x), TangentLine(f, x0, x)], x = xStart .. xFinish, 
  y = yStart .. yEnd, gridlines, size = [0.6, 0.6], 
  title = typeset("f(x) = ", f(x)), thickness = 7, 
  caption = typeset("Plot of tangent line at x = ", x0));

Question 2

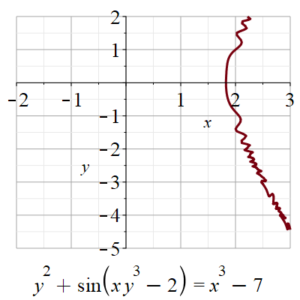
Using implicit differentiation find the equation of the tangent line to the graph of:

y^2 + \sin(xy^3 - 2) = x^3 - 7

which is shown in the above figure, at the point (x, y) = (2, 1). Then , to get credit for Question 2, find the x intercept of that tangent line to the nearest thousandth (3 decimal places).

Answer to Question 2:   the  x intercept of that tangent line  = \underline{\ \hspace{.75in}} .

 

Videos (6 parts) on how to solve Question 2.

Part 1. Review of the tangent line equation in the context of implicitly defined functions.

 

Part 2. Finding \frac{dy}{dx},  implicitly, for y^2 + \sin(xy^3 - 2) = x^3 - 7 .

 

Part 3. Finding \frac{dy}{dx},  implicitly, for y^2 + \sin(xy^3 - 2) = x^3 - 7 ; solving for \frac{dy}{dx}.

 

Part 4.  Evaluating \frac{dy}{dx} at  (x_0, y_0) = (2, 1).

 

Part 5.  Evaluating \frac{dy}{dx} at  (x_0, y_0) = (2, 1) continued, and finding the tangent line equation.

 

Part 6.  Finding the x intercept (which solves the Question 2).  In part 6, as an extra,  I  explain how to find the y intercept and how to graph the tangent line equation.

Answer to Question 2:   the  x intercept of that tangent line  = \underline{\ \ 1.273 \ } .

Note. Here is a graph of that tangent line:

 

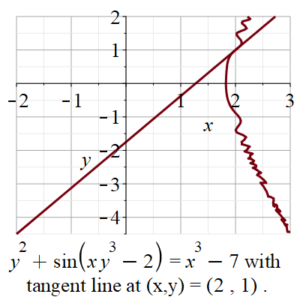
The following Maple commands will solve Question 2 and create the graph shown above.  You can copy and paste the following commands into Maple.

 restart:
with(plots):
implicit_f := y^2 + sin(x*y^3 - 2) = x^3 - 7;
x0 := 2;
y0 := 1;
xstart := -2:
xfinish := 3:
ystart := -5:
yfinish := 2:
"Check that (x0, y0) satisfies the implicit relation";
subs({x = x0, y = y0}, implicit_f);
implicit_diff_f := implicitdiff(implicit_f, y, x);
"tangent line equation y = mx + b at (x0, y0)";
m := evalf(subs({x = x0, y = y0}, implicit_diff_f));
b := -m*x0 + y0;
xintercept := -b/m;
implicitplot({implicit_f, y = m*x + b}, 
  x = xstart .. xfinish, y = ystart .. yfinish, thickness = 10,
  grid = [100, 100], gridlines, thickness = 3, rangeasview = true,
  size = [0.4, 0.7], 
  caption = typeset(y^2 + sin(x*y - 2) = x^3 - 7, 
    "and its tangent line at (", x0, ",", y0, ")."));

Question 3

You want to build a rectangular frame enclosing the maximum amount of area.
The top and bottom of the frame are going to be made out of gold (cost $ \$ $60 per centimeter) and the two sides of the frame are going to be made out of silver (cost $ \$ $4 per centimeter). You have $6,000 to spend. Find the maximum area your frame can enclose
to the nearest thousandth (three decimal places).

Video on how to solve Question 3. See end of the video for answer.

Question 3 is an example of what is called a constrained optimization problem. We want to optimize (maximize) the area enclosed by the frame  subject to the constraint of our budget being limited to $6,000.

Question 4

If f(x) = \ln(2x^3 + 9x + 6) + \sqrt{x + \sin\left(3x + \dfrac{\pi}{2}\right)} calculate   f'(0)  to
the nearest thousandth (three decimal places).

Make sure your calculator is set to radian measure.

Your answer should be a single number like
-9.123 or 8.789.

Video on how to solve Question 4. See end of the video for answer.

To solve Question 4 you need to know the following derivative formulas:

\frac{d}{dx} \ln u(x) = \dfrac{u'(x)}{u(x)}.

\frac{d}{dx} \sin u(x) = u'(x)\cos u(x).

Chain rule: \frac{d}{dx} f(g(x)) = f'(g(x))g'(x).

Power rule:  \frac{d}{dx} x^n = n x^{n-1} .

Combining the power rule with the chain rule give us:

\frac{d}{dx} \sqrt{u(x)} = \frac{d}{dx} u(x)^{1/2} = \frac{1}{2} u(x)^{-1/2} u'(x) = -\dfrac{u'(x)}{2 \sqrt{u(x)}}

Question 5

If f(x) = x^{3} e^{7x} + x^{-3} calculate   f'(1)  to
the nearest thousandth (three decimal places).

Your answer should be a single number like
-9.123 or 8.789.

Video on how to solve Question 5. See end of the video for answer.

 

Question 6

Suppose x^2 y^2 + y^2 = 3 + xy implicitly defines  y(x) .  Using implicit differentiation calculate  \dfrac{dy}{dx} at  (x,y) = (2, 1)  to the nearest thousandth (3 decimal places).

Your answer should be a single number like
-9.123 or 8.789.

Video (in two parts) on how to solve Question 6.
See end of the Part II video for answer.

Part I

 

Part II

 

Notes.

When we do implicit differentiation we assume that that y can be written as a function of x, in other words, y = y(x) and then we use the chain rule:   \frac{d}{dx} f(g(x) = f'(g(x))g'(x).

Some examples:

\frac{d}{dx} y^2 = 2y y'.

\frac{d}{dx} \sin(y) = \cos(y)y'.

An example which uses the product rule:

\frac{d}{dx} \left(fg\right) = f'g + fg'.

\frac{d}{dx} xy^2 = y^2 + 2xyy'.

Question 7

Supposef(x) = e^{3x} + \ln(4x) + \arccos(5x) + \sin(6x). Calculate  f'(0.1) to the nearest thousandth (3 decimal places).

Your answer should be a single number like
-9.123 or 8.789.

Video on how to solve Question 7. See end of the video for answer.

 

To solve Question 7 you need to know the following derivative formulas:

\frac{d}{dx} (f(x) + g(x)) = f'(x) + g'(x) .

\frac{d}{dx} e^{u(x)} = u'(x) e^{u(x)} .

\frac{d}{dx} \ln u(x) = \dfrac{u'(x)}{u(x)}.

\frac{d}{dx} \arccos u(x) = -\dfrac{u'(x)}{\sqrt{1 - (u(x))^2}}.

\frac{d}{dx} \sin u(x) = u'(x) \cos u(x).

Attribution-NonCommercial-ShareAlike 4.0 International

This entry is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International license.