Right hand rule and positive orientation

Stokes’ Theorem:

Let $ r: (u,v) \in D \rightarrow S $ parameterize the surface S. So,

$$r(u,v) =\left( x(u,v), y(u,v), z(u,v)  \right)  \  \   \text{ and }  \  \  r(D) = S $$

Let $c$ be the boundary of the surface S. Let $F(x, y, z)$ be a vector field on S.

If the surface normal vector  $\left(\dfrac{\partial r}{\partial u} \times \dfrac{\partial r}{\partial v}\right)(u, v)$ is positively oriented respect to the orientation (direction) of $c$ then Stokes’ theorem is true:

$$ \oint_c F \cdot dl = \iint_D (\nabla \times F)\left(r(u,v)\right) \cdot \left(\dfrac{\partial r}{\partial u} \times \dfrac{\partial r}{\partial v}\right)(u, v)\, dA $$

However, if the surface normal vector  $\left(\dfrac{\partial r}{\partial u} \times \dfrac{\partial r}{\partial v}\right)(u, v)$ is negatively oriented respect to the orientation (direction) of $c$ then to make Stokes’ theorem is true we need to multiply
$\left(\dfrac{\partial r}{\partial u} \times \dfrac{\partial r}{\partial v}\right)(u, v)$ by -1 to make Stokes’ Theorem true.

So, to apply Stokes Theorem we need to figure out if the surface normal vector  $\left(\dfrac{\partial r}{\partial u} \times \dfrac{\partial r}{\partial v}\right)(u, v)$ is positively oriented. If it isn’t, we need to multiply it by it -1.

The picture below shows how to use your right hand to determine the direction that the positively oriented surface normal should point, assuming that the boundary c of the surface S has been given an orientation.

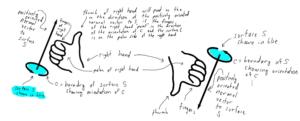
For additional information about the right hand rule and positive orientation of surfaces see Wikipedia (from which the public domain image “right hand rule grip” comes from):  https://en.wikipedia.org/wiki/Right-hand_rule

Another way to determine which direction the positively oriented surface normal vector should point is to imagine that you are walking along the boundary c of the surface S in the direction of the orientation of c with your LEFT side facing into the surface. Your head will point in the direction of positive orientation of the surface normal vector (relative to the orientation of c).  See images below.

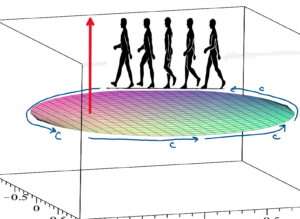
The red arrow shows the direction that the positively oriented surface normal vector (relative to the orientation of the boundary c) should point. Notice that the people are walking in the direction of c with their LEFT sides facing into the surface S (the colored disk) and so their “heads” are pointing in the direction of the positively oriented surface normal vector (the red arrow).

Remember, the surface normal vector is perpendicular to the surface, so that if the surface bends, the surface normal vector will change depending on where on the surface you are.

Also, the positively oriented surface normal vector doesn’t have to point in the “up direction”. For example, see the image below.

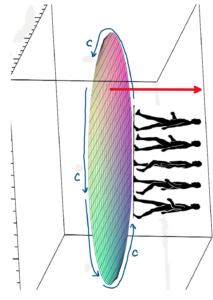
Note. The stick figures used in the above are in the public domain.

For more information about Stokes’ Theorem see Wikipedia:
https://en.wikipedia.org/wiki/Stokes%27_theorem

Stokes Theorem Questions

Question 1

Video of solution (2 parts).

Note. See the end of part 2 for the numerical solution and for notes about using the Maple script to solve this problem.

Part 1.

 

Part 2.

 

Maple code to solve Question 1.
Note: the Maple code assumes c and S are orientated according to the right hand rule. If they aren’t, you have to multiply the answer by -1.

restart;
with(plots):
with(LinearAlgebra):
# ------------------------------- Parameterize S
rx := (u, v) -> u^2 - v^2;
ry := (u, v) -> v*u;
rz := (u, v) -> u + v;
r := (u, v) -> <rx(u, v), ry(u, v), rz(u, v)>:
uRange := 0 .. 3;
vRange := 0 .. 2;
# ------------------------------- Vector Field F
"vector field F";
P := (x, y, z) -> 12*y^3;
Q := (x, y, z) -> 4*z;
R := (x, y, z) -> 6*x;
F := (x, y, z) -> <P(x, y, z), Q(x, y, z), R(x, y, z)>:
# ------------------------------- Plot S
s := plot3d([rx(u, v), ry(u, v), rz(u, v)], v = vRange, u = uRange, scaling = constrained, title = "The surface S in x,y,z space", labelfont = ["TimesNewRoman", 36], labels = ["x", "y", "z"], size = [600, 600]);
# ------------------------------- Calculate Normal Vector
ru := diff(r(u, v), u);
rv := diff(r(u, v), v);
print("Normal to surface (orientation of surface, i.e., direction of positive flux used in surface integral)");
ru_X_rv := CrossProduct(ru, rv);
# ------------------------------- Calculating Curf(F)
curlFP := (x, y, z) -> D[2](R)(x, y, z) - D[3](Q)(x, y, z):
curlFQ := (x, y, z) -> D[3](P)(x, y, z) - D[1](R)(x, y, z):
curlFR := (x, y, z) -> D[1](Q)(x, y, z) - D[2](P)(x, y, z):
curlF := (x, y, z) -> <curlFP(x, y, z), curlFQ(x, y, z), curlFR(x, y, z)>:
"curl of F at (x,y,z)";
curlF(x, y, z);
# ------------------------------- Integration
print("Integrand for surface flux integral");
curlF_dot_ru_X_rv := DotProduct(curlF(rx(u, v), ry(u, v), rz(u, v)), ru_X_rv, conjugate = false);
Int(Int(curlF_dot_ru_X_rv, u = uRange), v = vRange) = evalf(int(int(curlF_dot_ru_X_rv, u = uRange), v = vRange));  
# End of Maple Script 

Here is the output of the above Maple script.

Note that the numerical answer output by this Maple script will need to be multiplied by -1 (to solve Question 1) because the orientation of c (from the picture) and the surface normal vector (from the parameterization) did not follow the right hand rule in Question 1.

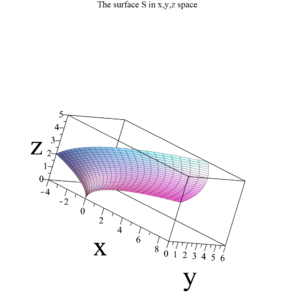
Note. The answer Maple gets -13,286.4 needs to be multiplied by -1. The Maple script is not set up to check orientation and it turns out (watch the video) that the surface normal vector $\left(\dfrac{\partial r}{\partial u} \times \dfrac{\partial r}{\partial v}\right)(u, v)$ in this problem was not positively oriented.

Here is a video of the surface S created by the above Maple script, being rotated.