Method of Undetermined Coefficients

Question 1

\displaystyle \ddot{x} + 6\dot{x} + 8x = 12t+30e^{-2t} ,   x(0) = 1, \ \ \dot{x}(0) = 3  

Solve the above IVP and then find

x(0.25)

Answer to Question 1 (see bottom of page for Maple and Matlab code):   

x(0.25)   = \underline{\ \hspace{.75in}} .

See video and graph below (in 3 parts) for solution.  Total run time about 18 minutes.
The answer is in Part 3.

Part 1.

 

 

Part 2.

 

 

Part 3.

 

 

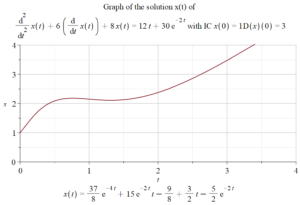
Below are the Maple commands to solve the IVP in Question 1 and create the above Figure.  You can copy and paste these commands into Maple.

 de := diff(x(t), t $ 2) + 6*diff(x(t), t) + 8*x(t) = 12*t + 30*exp(-2*t); 
tq := 0.25; 
ics := x(0) = 1, D(x)(0) = 3; 
SolutionIVP := dsolve({de, ics}); 
x(tq) = evalf(subs(t = tq, rhs(SolutionIVP))); 
plot(rhs(SolutionIVP), t = 0 .. 4, x = 0 .. 4, thickness = 2, size = [0.5, 0.6], gridlines, title = typeset("Graph of the solution x(t) of \n", de, " with IC ", ics), caption = typeset(SolutionIVP)); 
# End of Maple Script (Updated 2/9/2023)

Note for IC’s for higher order ODE’s.
Suppose we had a third order ODE with initial conditions of, say, x”(0) = 12, x'(0) = 3, and x(0) = 1. We would enter this in Maple as:

Very important. Do not forget to put the parenthesis around the 2 (see yellow highlighted command above).

Below is a screen capture of the commands to solve Question 1 in Maple.

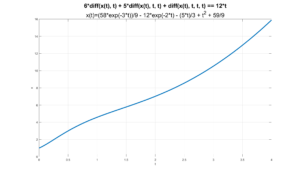
Matlab Solution to Question 1

Below are the Matlab commands to solve the IVP in Question 1 and create the above Figure.  You can copy and paste these commands into Matlab.

syms x(t);
Dx = diff(x,t);
ode = diff(x,t,2)+6*diff(x,t,1) + 8*x(t) == 12*t + 30*exp(-2*t)
cond1 = x(0) == 1;
cond2 = Dx(0) == 3;
conds = [cond1 cond2];
xSol(t) = dsolve(ode,conds)
tq = 2.5
xtq = eval(subs(xSol(t),t,tq))
fprintf('x(%f) = %f \n',tq,xtq)
xx = 0: .01: 4;
yy = eval(xSol(xx));
figure
plot(xx,yy, 'LineWidth',3)
grid on
title(string(ode), strcat("x(t)=",string(xSol(t))) )
ax = gca;
ax.TitleFontSizeMultiplier = 2
xlabel('t')
ylabel('x')

Note. You can make the font size smaller or larger by decreasing or increasing the value of ax.TitleFontSizeMultiplier.

Matlab Code for 3rd Degree Differential Equation with IC

Example. For the following IVP find x(t) and evaluate x(2.5).

x''' + 5 x'' + 6x' = 12t, \ \ \ \ x(0) = 1, x'(0) = 3, x''(0) = 12 .

Here is the Matlab Code to solve this example.

syms x(t);
Dx = diff(x,t);
D2x = diff(x,t,2);
ode = diff(x,t,3) + 5*diff(x,t,2)+6*diff(x,t,1) == 12*t;
cond1 = x(0) == 1;
cond2 = Dx(0) == 3;
cond3 = D2x(0) == 12;
conds = [cond1 cond2 cond3];
xSol(t) = dsolve(ode,conds)
tq = 2.5
xtq = eval(subs(xSol(t),t,tq))
fprintf('x(%f) = %f \n',tq,xtq)
xx = 0: .01: 4;
yy = eval(xSol(xx));
figure
plot(xx,yy, 'LineWidth',3)
grid on
title(string(ode), strcat("x(t)=",string(xSol(t))) )
ax = gca;
ax.TitleFontSizeMultiplier = 2
xlabel('t')
ylabel('x')
Here is the output of the Matlab solution:   x(2.500000) = 8.561598
Attribution-NonCommercial-ShareAlike 4.0 International

This entry is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International license.