Question 1

  .


Let    be the vector field on x, v phase space defined by

.

Find .

Answer to Question 1:   

  .

See video below for solution.  Total run time about 3 minutes 25 seconds.

 

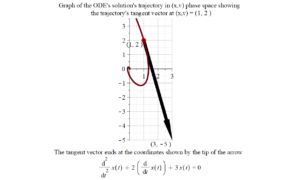
Graph for Question 1.

Important note.

We can easily find by subtraction if we know where the tangent vector   begins and where it ends.  If we look at the Figure above, we see that    begins at and ends at , hence:

.

Below are the Maple commands that created the above Figure (from Question 1).
You can copy and paste these commands into Maple.

with(plots):
with(VectorCalculus):
de := diff(x(t), t $ 2) + 2*diff(x(t), t $ 1) + 3*x(t) = 0;
xdot := (x, v) ->  v;
vdot := (x, v) -> -3*x - 2*v;
ics := x(0) = 1, D(x)(0) = 2;
SolutionIVP := dsolve({de, ics}):
xfun := t -> rhs(SolutionIVP):
x0 := rhs(ics[1]);
v0 := rhs(ics[2]);
"Tangent Vector";
Tx0 := xdot(x0, v0);
Tv0 := vdot(x0, v0);
EndTx0 := x0 + Tx0:
EndTv0 := v0 + Tv0:
plotA := plot([rhs(SolutionIVP), D(xfun)(t), t = -0.2 .. 12.6],
   thickness = 6, size = [0.5, 0.6], gridlines, 
   scaling = constrained, 
   title = typeset("Graph of the ODE's solution's trajectory in (x,v) phase space showing \n the trajectory's tangent vector at (x,v) = (", x0, ", ", v0, " )"), 
   caption = typeset("The tangent vector ends at the coordinates shown by the tip of the arrow \n ", de)):
plotB := pointplot([[rhs(ics[1]), rhs(ics[2])]], color = [red],
    symbol = solidcircle, symbolsize = 15):
plotC := textplot([rhs(ics[1]), rhs(ics[2]), 
   typeset("(", x0, ", ", v0, " )")], align = {'below', 'left'}):
plotD := textplot([EndTx0, EndTv0, typeset("(", EndTx0, ", ", EndTv0, " )")], align = {'below', 'left'}):
vs1 := VectorSpace('cartesian', [0, 0]):
vs2 := VectorSpace('cartesian', [x0, v0]):
plotE := PlotVector([vs2:-Vector([Tx0, Tv0])], width = 0.2):
display({plotA, plotB, plotC, plotD, plotE}); 

 

---

---