Question 1

,  

In the power series solution of the above IVP find the coefficient   of the    term.

 

Answer to Question 1:

See video below (in 3 parts) for solution as well as the comments, Figure, and Maple code under the last video.  Total run time of the video is about 17 minutes.

Part 1.

 

 

Part 2.

 

 

Part 3.

 

The nth order power series solution gives the nth order Taylor series approximation of the exact (actual) solution.  The approximation will be very good for values of x close to the initial condition. However as x increases, the approximation will tend to be less and less accurate.

In the Figure below, we compare the (exact) solution to the power series approximation we found in the video.  The approximation is good on the interval 0 < x < 1, however as soon as x > 1, the two solutions start to rapidly diverge.

 

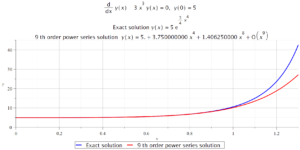
The following Maple commands will find the IVP solution and the 9th order power series approximate solution for Question 1 and create the graph shown above.
You can copy and paste the following commands into Maple.

restart;
ode := diff(y(x), x) - 3*x^3*y(x) = 0;
ic := y(0) = 5;
odeList := {ode};
icList := {ic};
dsys := odeList union icList;
Order := 9;
PS_sol := evalf(dsolve(dsys, y(x), series));
IVP_sol := dsolve(dsys);
x_start := 0;
x_end := 1.3;
y_start := 0;
y_end := 45;
plotA := plot([rhs(IVP_sol), rhs(PS_sol)], x = x_start .. x_end, y = y_start .. y_end, gridlines, color = [blue, red], title = typeset(ode, ", ", ic, "\n Exact solution ", IVP_sol, "\n", Order, "th order power series solution ", PS_sol), titlefont = ["HELVETICA", 24], legend = [typeset(" Exact solution "), typeset(Order, "th order power series solution ")], legendstyle = [font = ["HELVETICA", 24], location = bottom], thickness = 4, size = [0.7, 0.5]);
x_to_approx_y_at := 1.2;
printf("The %a th order power series approximation of y(%a) is:", Order, x_to_approx_y_at);
evalf(subs(x = x_to_approx_y_at, rhs(convert(PS_sol, polynom))));
printf("The exact value of y(%a) is:", x_to_approx_y_at);
evalf(subs(x = x_to_approx_y_at, rhs(convert(IVP_sol, polynom))));
# End of Maple Script

The above Maple script also outputs the solution to Question 2 (see below).

Question 2 is the same as Question 1, except in Question 2 you use the power series solution to approximate the value of $y(x)$.

Question 2

,  

With respect to the above IVP, find the $9^{th}$ order power series approximation of $y(1.2)$.

Note. To find the $9^{th}$ order power series approximation of $y(x)$, you have to find the power series solution up to and including the $x^8$ term. You don’t have to find the entire power series solution.

$y(1.2) \approx \underline{\hspace{1in}}$

Answer to Question 2:

To answer Question 2, we have to substitute $x = 1.2$ into the $9^{th}$ order power series solution from Question 1:

$$y(x) = 5 + 3.75 x^4 + 1.40625 x^8 + O(9)$$

We get:

$$y(1.2) \approx 5 + 3.75 (1.2)^4 + 1.40625 (1.2)^8  = 18.8226$$

So, the answer is

$y(1.2) \approx \underline{\hspace{.2in} 18.8226 \hspace{.2in}}$

Below, in red, is the by-hand calculation. The calculation starts at the end of the solution to Question 1.